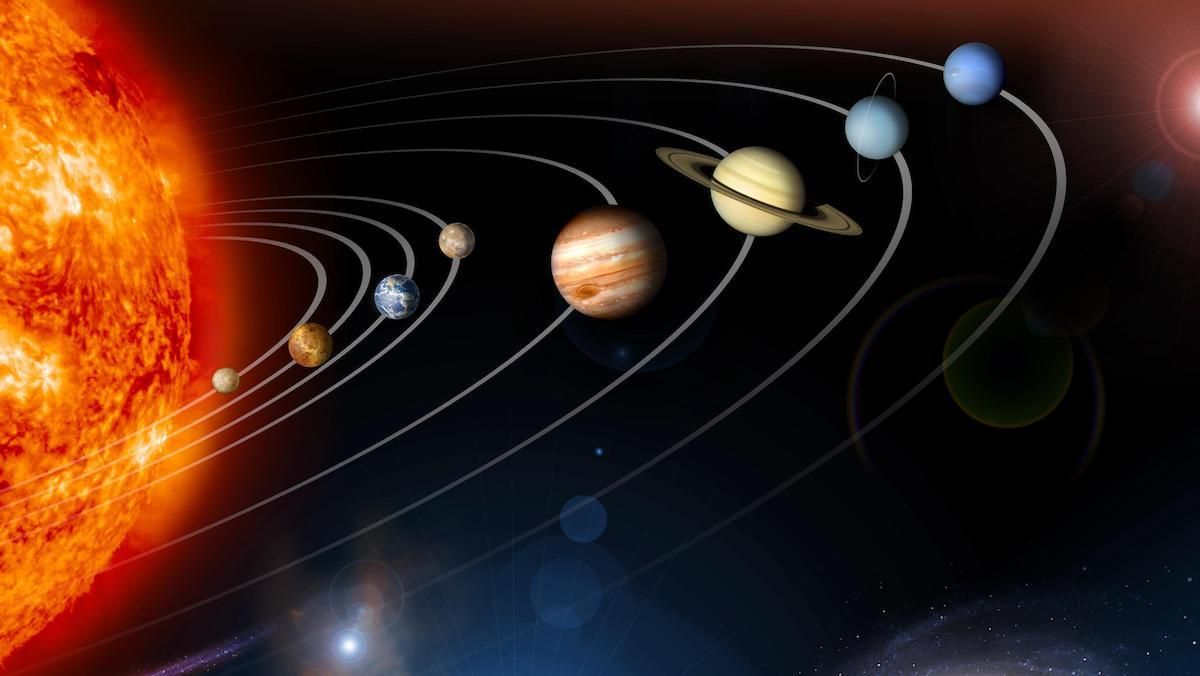
Движение, которое до формулирования третьего закона Кеплера было, по сути, загадкой (об этом мы немного рассказывали в предыдущей статье). Объясняем, что это за закон, о чем говорит, как возник и почему очень важен.
Также интересно Как приготовить горячий алкогольный коктейль Терпкий апельсин: попробовать себя в роли барMENа
Закон гармонии
Третий закон Кеплера появился в 1619 году и раскрыл механику Солнечной системы беспрецедентно подробно. Вот его формулировка: "Квадрат орбитального периода любой планеты пропорционален кубу большой полуоси ее орбиты". Это не так просто понять, если ты не астроном или математик, правда? Но не все так сложно, как кажется.
- Орбитальный период – это время, за которое планета делает один оборот вокруг звезды.
- А большая полуось орбиты планеты – это половина большой оси (самая длинная ось эллипса, между крайними точками узких полукругов, называется большой осью, а самая короткая – малой осью).
То есть, третий закон Кеплера сравнивает время вращения планеты вокруг звезды и радиус орбиты планеты, причем не только между собой, но и с такими же радиусами других планет. Так, в отличие от первого и второго законов Кеплера, описывающих характеристики движения одной планеты, третий закон астронома сравнивает движение разных планет и рассчитывает гармонию движения.
Модель эллиптической орбиты, точки фокусов и расстояния / Фото askamathematician
Так что благодаря этому закону, если мы знаем расстояние планеты от ее звезды, мы можем вычислить период ее орбиты – и наоборот. Для Солнечной системы это дает нам точное представление об орбите каждой планеты вокруг Солнца. К примеру,
- Расстояние между Землей и Солнцем – 149 миллионов километров (это как раз та самая "страшная" большая полуось орбиты нашей планеты или – одна астрономическая единица), а период обращения Земли вокруг Солнца – 365 дней. Соотношение по формуле третьего закона Кеплера – примерно 7,5 (для удобства показатель умножен на 10 в -6 степени).
- И тот же показатель мы увидим, если сравним расстояние до Солнца и период обращения любой другой планеты. Скажем, Меркурий – ближайшая к Солнцу планета – делает круг (точнее, эллипс) каждые 88 дней, расстояние до Солнца – 0,389 астрономической единицы. Если 0,389 в кубе разделить на 88 в квадрате – получим примерно 7,5.
Особое и особенно важное применение третьего закона Кеплера
В третьем законе Кеплера нет упоминания о массе объекта. Но именно благодаря ему и закону тяготения Ньютона физики дошли до более цельной формы уравнения. Уравнения, помогающего вычислять массы тел, фигурирующих в описанной системе.
Стоит знать Наш дом – галактика Млечный Путь, но откуда нам об этом известно
Вникать глубоко не будем, скажем только, что третий закон Кеплера успешно применили для определения точных масс планет в Солнечной системе и их средней плотности.
Также третий закон Кеплера полезен не только в Солнечной системе.
- Астрономы открыли уже более 4000 экзопланет (планет вне Солнечной системы), и благодаря законам Кеплера могут вычислить их орбиты и массы.
- Только с тем нюансом, что использовать для этого немного усовершенствованную формулу – с учетом массы звезды, вокруг которой вращается та или иная планета, в соотношении с массой нашего Солнца.
Дальше – больше. Законы Кеплера позволили ученым понять массы звезд в двойных системах, что в свою очередь позволяет больше узнать о структурах и эволюции звезд вообще.
Мог ли Иоганнес Кеплер в XVI веке хотя бы догадываться, в какую даль заведет всю мировую науку его увлечение наблюдением за кометой, не правда ли?